第22章-基本图算法
图的表示
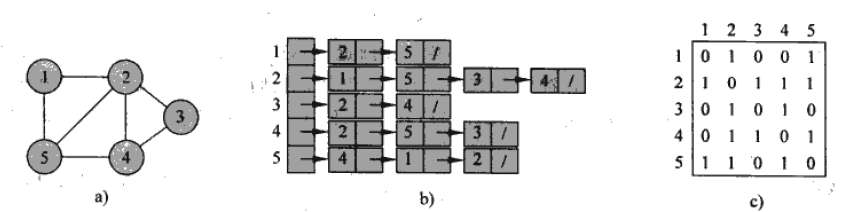
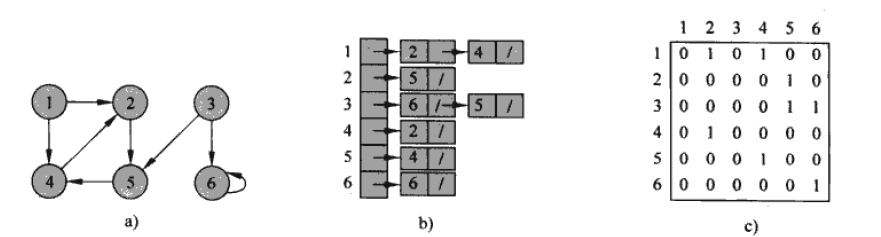
图\(G=(V, E)\),其中\(V\)表示结点,\(E\)表示边
邻接链表: 表示稀疏图时,非常紧凑
稀疏图:边的条数(\(|E|\))远远小于边的结点数(\(|V|\))的图
- 需要空间\(\Theta(E+V)\)
- 邻接表表示由一个包含\(|V|\)条链表的数组\(Adj\)所构成,对于结点\(u\in V\),\(Adj[u]\)表示图\(G\)中所有与\(u\)邻接的结点
邻接矩阵:能快速查询两个结点之间是否有相连
矩阵的行号表示起始点,列号表示终点
- 需要空间\(\Theta(V^2)\)
- 无向图的矩阵式一个对称矩阵,因为边\((u, v)\)和边\((v, u)\)是一样的
无向图的表示
有向图的表示
广度优先搜索
给定图\(G=(V, E)\)和一个源结点S,执行广度优先搜索的时候会生成一颗广度优先树。
对于结点\((u, v)\),在广度优先搜索树中,称结点\(u\)是结点\(v\)的前驱或者父结点
最短路径距离: \(\delta(s, v)\)为从结点\(s\)到结点\(v\)之间所有路径里面最少的边数,如果\(s\)和\(v\)之间没有路径相连,则\(\delta=\infty\)
总代价:\(O(E+V)\)
初始化操作的成本:O(V)
扫描邻接链表的时间:\(O(E)\)
算法为每个结点赋予了一点额外的属性, 以结点\(u\)为例
- \(u.color\):结点的颜色
- \(u.\pi\):结点前置结点
- \(u.d\): 结点到源节点的距离
def BFS(G, s): |
过程:
- 源头结点设置color=灰色,d=0, \(\pi\)=NIL, 其他结点color = 白色,d = 正无穷, \(\pi\)=NIL
- 创建一个FIFO队列,放入源结点
- 循环从队列中取结点\(u\)
- 迭代\(u\)的邻接列表,获得结点\(v\)
- 如果\(v\)的颜色是白色,讲其颜色改为灰色,然后距离+1,前置设置为\(u\)
- 将\(v\)放入队列
- 将\(u\)的颜色改为黑色(队列中取出的颜色都是灰色,所以这里都是将灰色->黑色)
深度优先搜索
广度优先搜索的前驱子图形成一颗树,而深度优先搜索的前驱子图可能由多棵树组成,因为搜索可能从多个源结点重复进行。
深度优先搜索的前驱子图,设图\(G_\pi = (V, E_\pi)\),其中\(E_\pi = {(v.\pi, v), v \in V 且 v.\pi \neq NIL}\)。
所有的深度优先树是不相交的
深度优先搜索中结点的属性略有不同:
- \(u.color\)
- \(u.pi\)
- \(u.d\):记录发现结点\(u\)的时刻
- \(u.f\):记录完成结点\(u\)的时刻
步骤:
- 所有结点涂成白色, \(v.\pi=NIL\),时间time=0
- 循环图中每个结点\(u\),
如果结点颜色是白色:
- time=time+1, \(u\)的颜色变为灰色
- 循环G图中\(u\)结点邻接链表的每个结点\(v\), 如果\(v.color\)是白色,重复上面的操作
- \(u\)的颜色改为黑色,time=time+1, \(u\)设置完成时间
def DFS(G): |
深度优先探索的性质
- 前驱子图\(G_\pi\)形成一个由多棵树所构成的森林
- 结点的发现时间和完成时间具有所谓的括号化结构
边的分类
- 树边:为深度森林\(G_\pi\)的边。如果结点\(v\)是因为算法对边\((u, v )\)的探索而首先呗发现,则\((u. v)\)是一条树边.
- 后向边:后向边\((u, v)\)是将结点\(u\)连接到其在深度优先树中祖先结点\(v\)的边
- 前向边:后向边\((u, v)\)是将结点\(u\)连接到其在深度优先树中后代结点\(v\)的边
- 横向边:其他所有的边
拓补排序
对于一个有向无环图\(G=(V, E)\),来说,其拓补排序是\(G\)中所有结点的一种线性次序
def TOPOLOGICAL_SORT(G): |
强连通分量
深度搜索的经典应用:将有向图分解为强连通分量。
有向有环图中,环中的每个结点都可以确保访问。所以将环抽象为一个结点。
有向图\(G=(U, V)\)的强连通分量是一个最大结点集合\(C \subseteq U\), 对越该结点中任意两个结点\(u\), \(v\)来说,路径\(u\leadsto v\)和路径 \(v \leadsto u\)同时存在。
步骤:
- 使用DFS计算图G每个结点的结束时间
- 计算图\(G\)的转置\(G^T\)
- 使用DFS计算\(G^T\),但是在循环中,根据之前计算的每个结点的结束时间倒序。
- 将上一步获得的每一个深度搜索树返回,就是每个强连通分量。
练习
22.1-1
给定一个有向图的邻接表表示,计算该图中每个顶点的出度(发出的边的条数)需要多少时间?计算每个顶点的入度(进入的边的条数)需要多少时间?
\(O(|E|+|V|)\)
22.1-2
给出一个包含7个顶点的完全二叉树的邻接表表示,写出其等价的邻接矩阵表示。假设各个顶点如在一个二项堆中一样,从1到7进行编号。
因为完全二叉树
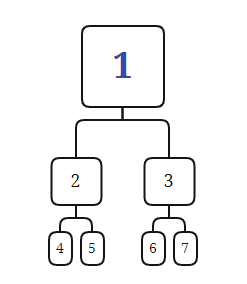
所以邻接链表: \[1 \rightarrow 2 \rightarrow 3 \] \[2 \rightarrow 1 \rightarrow 4 \rightarrow 5 \] \[3 \rightarrow 1 \rightarrow 6 \rightarrow 7 \] \[4 \rightarrow 2 \] \[5 \rightarrow 2 \] \[6 \rightarrow 3 \] \[7 \rightarrow 3\] 邻接矩阵:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
|---|---|---|---|---|---|---|---|
| 1 | 0 | 1 | 1 | 0 | 0 | 0 | 0 |
| 2 | 1 | 0 | 0 | 1 | 1 | 0 | 0 |
| 3 | 1 | 0 | 0 | 0 | 0 | 1 | 1 |
| 4 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| 5 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| 6 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| 7 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
22.1-3

# 链表 |
运行时间分别为:
- \(O(|E|+|V|)\)
- \(O(|V|^2)\)
22.1-4
给定一个多重图\(G=(V,E)\)的邻接表(多图是允许重复边和自循环边的图)表示,给出一个具有O(V+E)时间的算法,来计算其“等价”的无向图\(G'=(V,E')\)的邻接表表示,其中\(E'\)是将\(E\)中的冗余边和自循环边删除后余下的边。删除冗余边值得是将两个结点之间的多条边替换为一条边。
def clean_graph(G): |
22.1-5
有向图\(G=(V,E)\)的平方图是图\(G^2=(V,E^2)\),这里,边\((u,v)\in E^2\)当且仅当图\(G\)包含一条最多由两条边构成的从\(u\)到\(v\)的路径。请给出一个有效算法来计算图\(G\)的平方图\(G^2\).这里图\(G\)既可以以邻接链表表示,也可以以邻接矩阵表示,请分析算法的运行时间
答:
def square(G): |
22.1-6
多数以邻接矩阵作为输入的图算法的运行时间为\(\Omega(V^2)\),但也有例外。给定图G的邻接矩阵表示,请给出一个\(O(V)\)时间的算法来判断有向图G是否存在一个通用汇点( universal sink)。通用汇点指的是入度为\(|V|-1\)但出度为0的结点
答:
在矩阵中从(1,1)开始寻找。如果值是1,就下一行(因为出度为0),如果是0,就检查转置的位置是否是1
def find_universal_sink(G): |
22.1-7

答: \[ B\cdot B^T(i, j)=\sum_{e\in E}{}b_{ie}b_{ej}^T = \sum_{e\in E}{}b_{ie}b_{je} \] 所以
- 如果 i == j,则\(b_{ie}b_{je} = 1\)(当边\(e\)经过\(i,j\)的时候)或者0(边\(e\)不经过\(i, j\))
- 如果 i != j,则\(b_{ie}b_{je}= -1\)(当点\(i, j\)是边\(e\)的两端的时候)或者0(点\(i, j\)不是边\(e\)的两端的时候)
所以 \[ B\cdot B^T(i, j) = \begin{cases} 经过i的边的数目, \quad i==j \\ -(连接i, j的边的数目), \quad i!=j \end{cases} \]
22.1-8

答:\(O(1)\)
22.2-1
请计算出在有向图22-2(a)上运行广度优先搜索算法后的\(d\)值和\(\pi\)值。这里假定结点3为算法所用的源结点
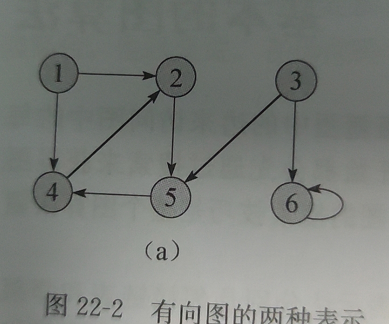
| 1 | 2 | 3 | 4 | 5 | 6 | |
|---|---|---|---|---|---|---|
| \(d\) | \(\infty\) | 3 | 0 | 2 | 1 | 1 |
| \(\pi\) | NIL | 4 | NIL | 5 | 3 | 3 |
22.2-2
请计算出在图22-3所示无向图上运行广度优先搜索算法后的\(d\)值和\(\pi\)值。这里假定结点\(u\)为算法所用的源结点

| \(r\) | \(s\) | \(t\) | \(u\) | \(v\) | \(w\) | \(x\) | \(y\) | |
|---|---|---|---|---|---|---|---|---|
| \(d\) | 4 | 3 | 1 | 0 | 5 | 2 | 1 | 1 |
| \(\pi\) | \(s\) | \(w\) | \(u\) | NIL | \(r\) | \(t\) | \(u\) | \(u\) |
22.2-3
证明:使用单个位来存放每个结点的颜色即可。这个论点可以通过证明将算法第18行的伪代码删除后,BFS过程生成的结果不变来得到。
答:因为循环值判断颜色是不是白色,所以算法是可以删除18行(最后将完成得到结点变为黑色)
22.2-4
如果将输入的图用邻接矩阵来表示,并修改算法来应对此种形式的输入,请问BFS的运行时间将是多少?
答:初始化成本变高,从原来的\(O(E)\)升高到\(O(V^2)\),所以最后运行时间为\(O(V^2 + V)\)
22.2-5
证明:在广度优先搜索算法里,赋给结点\(u\)的\(u.d\)值与结点在邻接链表里出现的次序无关。使用图22-3作为例子,证明:BFS所计算出的广度优先树可以因邻接链表中的次序不同而不同。
答:
22.2-6
举出一个有向图\(G=(V,E)\)的例子,对于源结点\(s∈V\)和一组树边\(E_\pi \in E\),使得对于每个结点\(v∈V\),图\((V,E_\pi)\)中从源结点\(s\)到结点\(v\)的唯一简单路径也是图G中的一条最短路径,但是,不管邻接链表里结点之间的次序如何,边集\(E_\pi\)都不能通过在图\(G\)上运行BFS来获得。
答:
22.2-7
职业摔跤手可以分为两种类型:“娃娃脸”(“好人”)型和“高跟鞋”(“坏人”)型。在任意对职业摔跤手之间都有可能存在竞争关系。假定有n个职业摔跤手,并且有一个给出竞争关系的r对摔跤手的链表。请给出一个时间为\(O(n+r)\)的算法来判断是否可以将某些摔跤手划分为“娃娃脸”型,而剩下的划分为“高跟鞋”型,使得所有的竞争关系均只存在于娃娃脸型和高跟鞋型选手之间。如果可以进行这种划分,则算法还应当生成一种这样的划分。
答:广度优先搜索,标记每个结点的颜色为"好人"或者“坏人”,然后交替连接好人坏人。时间:\(O(n+r) + O(r) = O(n + r)\)
22.2-8*
我们将一棵树\(T=(V,E)\)的直径定义为 \(max_{u,v\in V}\delta(u,v)\),也就是说,树中所有最短路径距离的最大值即为树的直径。请给出一个有效算法来计算树的直径,并分析算法的运行时间
答:
22.2-9
设\(G=(V,E)\)为一个连通无向图。请给出一个\(O(V+E)\)时间的算法来计算图G中的条这样的路径:该路径正反向通过E中每条边恰好一次(该路径通过每条边两次,但这两次的方向相反)。如果给你大量的分币作为奖励,请描述如何在迷宫中找出一条路。
答:
def find(u): |
22.3-1
答: