第24章-单源最短路径

发表于 更新于 分类于 阅读次数： 本文字数： 967 阅读时长 ≈ 4 分钟

单源最短路径

环路

前驱结点

前驱子图

松弛操作

松弛（relaxation）技术：对于每个结点\(v\)来说，我们维持一个属性\(v.d\)，用来记录从源结点\(s\)到结点\(v\)的最短路径权重的上界。我们称\(v.d\)为s到\(v\)的最短路径估计

最短路径估计和前驱结点进行初始化:

INITIALIZE-SINGLE-SOURCE(G, s):
	for each vertex v in G.V
		v.d = infty 
		v.pi = NIL 
	s.d = 0

对一条边（\(u\), \(v\)）的松弛过程:

  • 测试是否可以对\(s\)到\(v\)的最短距离进行改善
    • 将\(s\)到\(u\)的最短路径，加上结点\(u\)到\(v\)的权重,与当前\(s\)到\(v\)的最短距离进行比较
    • 如果前者更小，则更新\(v.d\)和\(v.\pi\)
RELAX(u, v, w):
	if v.d > u.d + w(u, v):
		v.d = u.d + w(u, v)
		v.pi = u

其中 w(u, v)表示：点u到点v的权重 v.d: 表示从源s到v的最短距离 v.pi: 表示v的上一个节点

松弛操作和最短路径的性质

  • 三角不等式性质
  • 上界性质
  • 非路径性质
  • 收敛性质
  • 路径松弛性质
  • 前驱子图性质

Bellman-Ford算法

边的权重可以为负值

给定带权重的有向图\(G=(V, E)\)和权重函数\(w: E\rightarrow R\)

算法返回一个布尔值

  • 如果存在权重为负值的环路，返回false（负值的环路，不停的循环，可以使总权重一直降低）
  • 反之，给出最短路径和他们的权重
BELLMAN-FORD(G, w, s):
	INITIALIZE-SINGLE-SOURCE(G, s)
	for i=1 to |G.V| - 1
		for each edge(u, v) in G.E
			RELAX(u, v)
	for each edge(u, v) in G.E
		if u.d > v.d + w(u, v):
			return False
	return True

有向无环图中的单源最短路径问题

Dijkstra算法

差分约束和最短路径

最短路径的证明

练习

24.1-1

在图24-4中运行Bellman-Ford算法,使用结点\(z\)作为源结点。在每一遍松弛过程中以图中相同的次序对每条边进行松弛，给出每遍松弛操作后的\(d\)值和\(\pi\)值。然后，把边\((z, x)\)的权重改为4， 再次运行该算法，这次使用\(s\)作为结点。

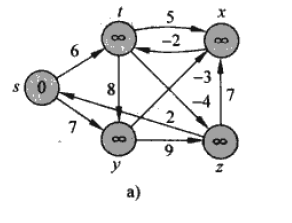
使用\(z\)作为源节点：

\(d\)的值:

松弛次数 \(s\) \(t\) \(x\) \(y\) \(z\)
0 \(\infty\) \(\infty\) \(\infty\) \(\infty\) 0
1 2 \(\infty\) 7 \(\infty\) 0
2 2 5 7 9 0
3 2 5 6 9 0
4 2 4 6 9 0

\(\pi\)的值：

\(s\) \(t\) \(x\) \(y\) \(z\)
NIL NIL NIL NIL NIL
\(z\) NIL \(x\) NIL NIL
\(z\) \(x\) \(x\) \(s\) NIL
\(z\) \(x\) \(y\) \(s\) NIL
\(z\) \(x\) \(y\) \(s\) NIL

修改权重之后

24.1-2

证明推论24.3

证明:

24.1-3

给定\(G=(V, E)\)是一个带权重且没有权重为负值的环路的有向图，对于所有结点\(v\in V\)，从源结点\(s\)到结点\(v\)之间的最短路径中，包含边的条数的最大值为\(m\)。（这里，判断最短路径的根据是权重，不是边的条数。）请对算法BELLMAN-FORD进行简单修改，可以让其在\(m+1\)遍松弛操作之后种植，即使\(m\)不是事先知道的一个值。

24.1-4

修改BELLMAN-FORD算法，使其对于所有结点v来说，如果从源节点\(s\)到结点\(v\)的一条路径上存在权重为负值的环路，则将\(v.d\)的值设置为\(-\infty\)

24.1-5

设\(G=(V, E)\)为一个带权重的有向图，其权重函数为\(w: E \rightarrow R\)。请给出一个时间复杂度为\(O(VE)\)的算法，对于每个结点\(v \in V\)，计算出数值$^*(v) = {(u, v)} $

24.1-6

假定\(G=(V, E)\)为一个带权重的有向图，并且图中存在一个权重为负值的环路。给出与i个有限的算法来列出所有该环路上的结点。请证明算法的正确性。

思考题